Intro To B-Trees

I first heard of the data structure in Martin Kleppmann's book, Designing Data Intensive Applications. At the time I didn't investigate further, however, a recent spark of interest in distributed systems has led me

It turns out B-Trees most SQL based database systems and is used for indexing in NOSQL based systems as well. Every time you write that SELECT or INSERT command and run it against a MySQL server, it's fetching that data from a B-Tree or some modified version of the base data structure.

Now that their importance has been established, I feel, like every other textbook on this topic does, it's useful to look at a Binary Search Tree (BST).

Visually, this is a BST:

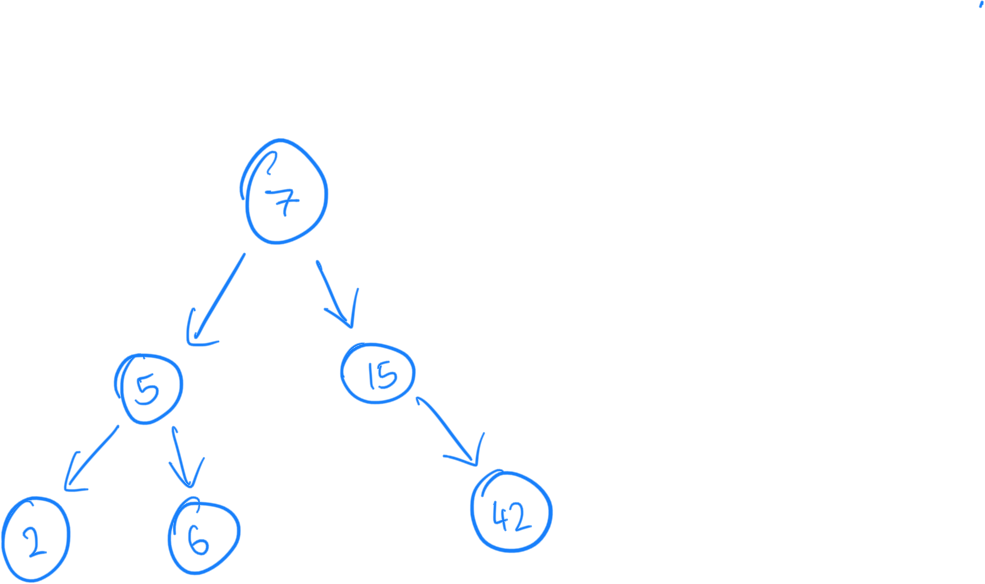
In BSTs, the left child contains a value smaller than the parent, and the right side has a value greater than the parent. Having the data in order enables us to search very fast.

Specifically, in logarithmic time. If you had to search through a billion items, you could find your item in about 9 iterations.

Not all BSTs trees are constructed equally. The first picture shows a balanced tree, in simplistic terms means there isn't a large height difference between the children.

If your tree isn't balanced, like the figure below, the search won't be very fast.

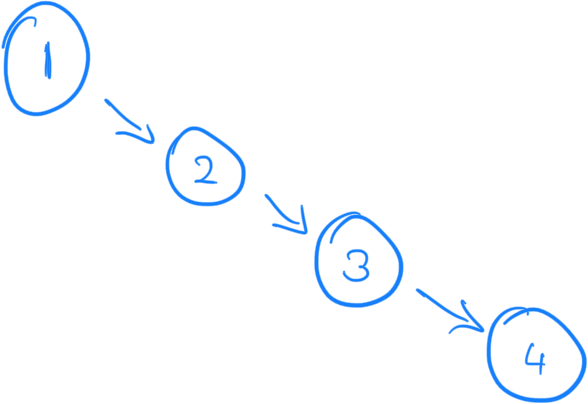
Search is now in linear time, as it resembles a linked list. To optimize for search in a BST we need to ensure it's balanced whenever we add, remove, or update nodes.

Balancing isn't cheap. It not only takes extra CPU cycles but you now need to update the tree structure on disk, where it is stored. Disk access is magnitudes slower than memory access. Your application that has millions of users on it wouldn't even function.

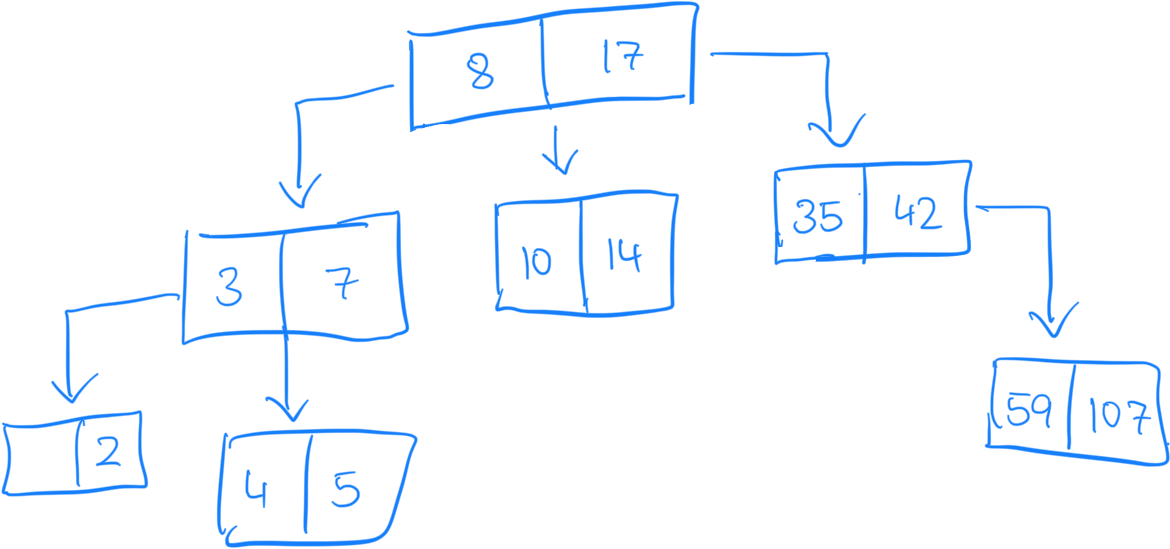
Smart people have already thought about this. Balancing doesn't happen often if each node had 2 keys with 3 children. These are called 2-3 trees.

Similar to BSTs, keys smaller than all keys in the parent are sent to the left child. Values in-between the two parent keys are sent to the middle one. Everything greater than the parent goes to the right. Balancing is a more expensive operation however it's expected to happen less frequently.

Here's an example of a 2-3 Tree:

Now why stop here? Why not add as many keys as you want in a node?

And that is what a B-Tree is. It's a balanced tree where each node can have n keys with n + 1 children. You can have 4-5 trees or even 1000-1001 trees. It's up to the implementer to decide.

A visual representation looks something like this:

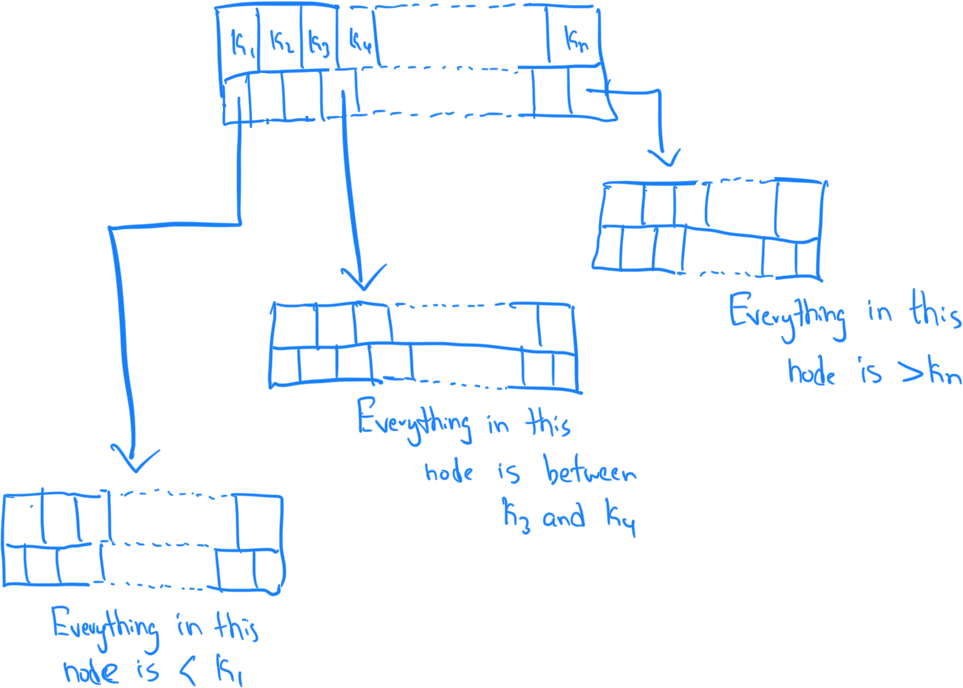
Balancing is a rare operation as the number of keys increases and every balance is very expensive. This is an acceptable trade-off and allows us to build highly optimized and scalable databases.

Most production-grade systems build upon this initial concept of B-Trees and are tailored for disk storage and concurrency. We won't get into the many adaptations of B-Tree in this article (partly because I have no idea about it).

That's it for this post, hope you learned something. I'll see you next week.